Fixed Budget is No Harder Than Fixed Confidence in Best-Arm Identification up to Logarithmic Factors

The best-arm identification (BAI) problem is one of the most fundamental problems in interactive machine learning, which has two flavors: the fixed-budget setting (FB) and the fixed-confidence setting (FC). For $K$-armed bandits with the unique best arm, the optimal sample complexities for both settings have been settled down, and they match up to logarithmic factors. This prompts an interesting research question about the generic, potentially structured BAI problems: Is FB harder than FC or the other way around? In this paper, we show that FB is no harder than FC up to logarithmic factors. We do this constructively: we propose a novel algorithm called FC2FB (fixed confidence to fixed budget), which is a meta algorithm that takes in an FC algorithm $\mathcal{A}$ and turn it into an FB algorithm. We prove that this FC2FB enjoys a sample complexity that matches, up to logarithmic factors, that of the sample complexity of $\mathcal{A}$. This means that the optimal FC sample complexity is an upper bound of the optimal FB sample complexity up to logarithmic factors. Our result not only reveals a fundamental relationship between FB and FC, but also has a significant implication: FC2FB, combined with existing state-of-the-art FC algorithms, leads to improved sample complexity for a number of FB problems.

Counterfactual Evaluation of Ads Ranking Models through Domain Adaptation

We propose a domain-adapted reward model that works alongside an Offline A/B testing system for evaluating ranking models. This approach effectively measures reward for ranking model changes in large-scale Ads recommender systems, where model-free methods like IPS are not feasible. Our experiments demonstrate that the proposed technique outperforms both the vanilla IPS method and approaches using non-generalized reward models.

Best of Three Worlds: Adaptive Experimentation for Digital Marketing in Practice

Adaptive experimental design (AED) methods are increasingly being used in industry as a tool to boost testing throughput or reduce experimentation cost relative to traditional A/B/N testing methods. However, the behavior and guarantees of such methods are not well-understood beyond idealized stationary settings. This paper shares lessons learned regarding the challenges of naively using AED systems in industrial settings where non-stationarity is prevalent, while also providing perspectives on the proper objectives and system specifications in such settings. We developed an AED framework for counterfactual inference based on these experiences, and tested it in a commercial environment.

A Data-Driven State Aggregation Approach for Dynamic Discrete Choice Models

We study dynamic discrete choice models, where a commonly studied problem involves estimating parameters of agent reward functions (also known as "structural" parameters), using agent behavioral data. Maximum likelihood estimation for such models requires dynamic programming, which is limited by the curse of dimensionality. In this work, we present a novel algorithm that provides a data-driven method for selecting and aggregating states, which lowers the computational and sample complexity of estimation. Our method works in two stages. In the first stage, we use a flexible inverse reinforcement learning approach to estimate agent Q-functions. We use these estimated Q-functions, along with a clustering algorithm, to select a subset of states that are the most pivotal for driving changes in Q-functions. In the second stage, with these selected "aggregated" states, we conduct maximum likelihood estimation using a commonly used nested fixed-point algorithm. The proposed two-stage approach mitigates the curse of dimensionality by reducing the problem dimension. Theoretically, we derive finite-sample bounds on the associated estimation error, which also characterize the trade-off of computational complexity, estimation error, and sample complexity. We demonstrate the empirical performance of the algorithm in two classic dynamic discrete choice estimation applications.

Neural Insights for Digital Marketing Content Design

In digital marketing, experimenting with new website content is one of the key levers to improve customer engagement. However, creating successful marketing content is a manual and time-consuming process that lacks clear guiding principles. This paper seeks to close the loop between content creation and online experimentation by offering marketers AI-driven actionable insights based on historical data to improve their creative process. We present a neural-network-based system that scores and extracts insights from a marketing content design, namely, a multimodal neural network predicts the attractiveness of marketing contents, and a post-hoc attribution method generates actionable insights for marketers to improve their content in specific marketing locations. Our insights not only point out the advantages and drawbacks of a given current content, but also provide design recommendations based on historical data. We show that our scoring model and insights work well both quantitatively and qualitatively.

Adaptive Experimental Design and Counterfactual Inference

Adaptive experimental design methods are increasingly being used in industry as a tool to boost testing throughput or reduce experimentation cost relative to traditional A/B/N testing methods. This paper shares lessons learned regarding the challenges and pitfalls of naively using adaptive experimentation systems in industrial settings where non-stationarity is prevalent, while also providing perspectives on the proper objectives and system specifications in these settings. We developed an adaptive experimental design framework for counterfactual inference based on these experiences, and tested it in a commercial environment.

Instance-optimal PAC Algorithms for Contextual Bandits

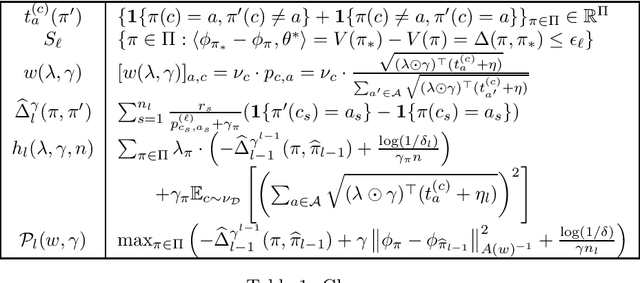
In the stochastic contextual bandit setting, regret-minimizing algorithms have been extensively researched, but their instance-minimizing best-arm identification counterparts remain seldom studied. In this work, we focus on the stochastic bandit problem in the $(\epsilon,\delta)$-$\textit{PAC}$ setting: given a policy class $\Pi$ the goal of the learner is to return a policy $\pi\in \Pi$ whose expected reward is within $\epsilon$ of the optimal policy with probability greater than $1-\delta$. We characterize the first $\textit{instance-dependent}$ PAC sample complexity of contextual bandits through a quantity $\rho_{\Pi}$, and provide matching upper and lower bounds in terms of $\rho_{\Pi}$ for the agnostic and linear contextual best-arm identification settings. We show that no algorithm can be simultaneously minimax-optimal for regret minimization and instance-dependent PAC for best-arm identification. Our main result is a new instance-optimal and computationally efficient algorithm that relies on a polynomial number of calls to an argmax oracle.

Improved Confidence Bounds for the Linear Logistic Model and Applications to Linear Bandits

We propose improved fixed-design confidence bounds for the linear logistic model. Our bounds significantly improve upon the state-of-the-art bounds of Li et al. (2017) by leveraging the self-concordance of the logistic loss inspired by Faury et al. (2020). Specifically, our confidence width does not scale with the problem dependent parameter $1/\kappa$, where $\kappa$ is the worst-case variance of an arm reward. At worse, $\kappa$ scales exponentially with the norm of the unknown linear parameter $\theta^*$. Instead, our bound scales directly on the local variance induced by $\theta^*$. We present two applications of our novel bounds on two logistic bandit problems: regret minimization and pure exploration. Our analysis shows that the new confidence bounds improve upon previous state-of-the-art performance guarantees.

Deep PQR: Solving Inverse Reinforcement Learning using Anchor Actions

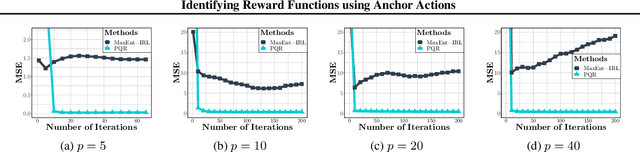
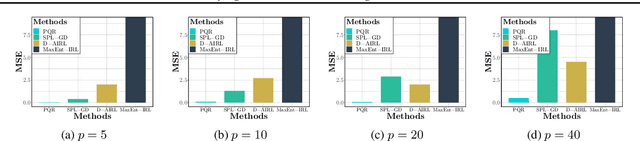
We propose a reward function estimation framework for inverse reinforcement learning with deep energy-based policies. We name our method PQR, as it sequentially estimates the Policy, the $Q$-function, and the Reward function by deep learning. PQR does not assume that the reward solely depends on the state, instead it allows for a dependency on the choice of action. Moreover, PQR allows for stochastic state transitions. To accomplish this, we assume the existence of one anchor action whose reward is known, typically the action of doing nothing, yielding no reward. We present both estimators and algorithms for the PQR method. When the environment transition is known, we prove that the PQR reward estimator uniquely recovers the true reward. With unknown transitions, we bound the estimation error of PQR. Finally, the performance of PQR is demonstrated by synthetic and real-world datasets.

Decoupling Learning Rates Using Empirical Bayes Priors

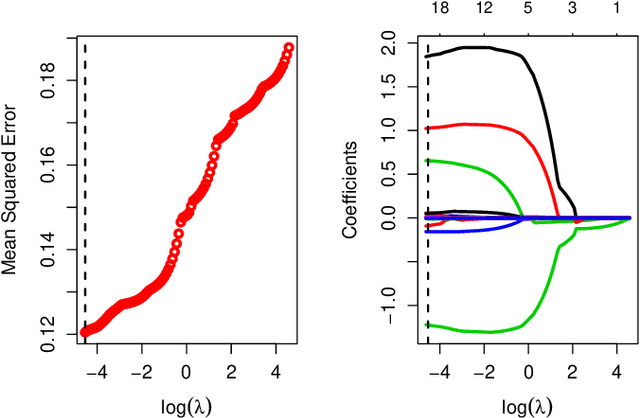
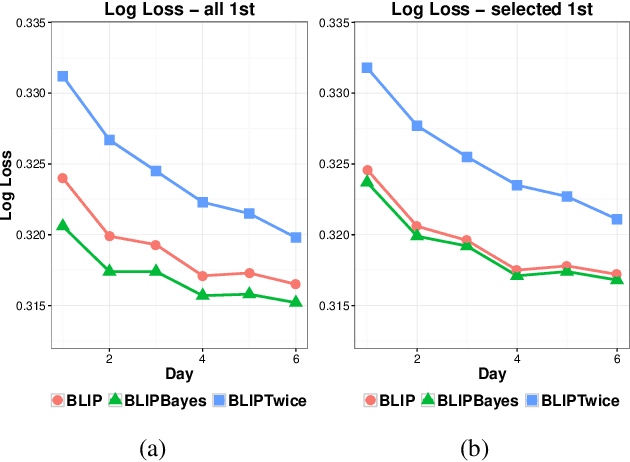
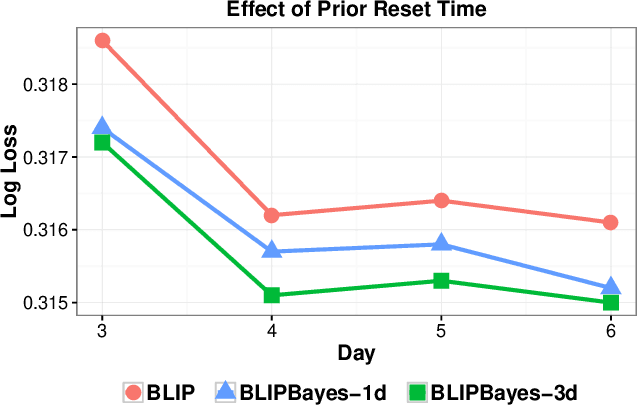
In this work, we propose an Empirical Bayes approach to decouple the learning rates of first order and second order features (or any other feature grouping) in a Generalized Linear Model. Such needs arise in small-batch or low-traffic use-cases. As the first order features are likely to have a more pronounced effect on the outcome, focusing on learning first order weights first is likely to improve performance and convergence time. Our Empirical Bayes method clamps features in each group together and uses the observed data for the deployed model to empirically compute a hierarchical prior in hindsight. We apply our method to a standard classification setting, as well as a contextual bandit setting in an Amazon production system. Both during simulations and live experiments, our method shows marked improvements, especially in cases of small traffic. Our findings are promising, as optimizing over sparse data is often a challenge. Furthermore, our approach can be applied to any problem instance modeled as a Bayesian framework.